One Silly Integer Trick
Just a bit (or two) of fun.
2 in 1 shampoo is not real, because 1 is not big enough to hold 2. That's why 2 was created. If it was 2 in 1, it would be overflowing.
What you must learn is that these rules are no different than the rules of a computer system. Some of them can be bent. Others can be broken.
—Morpheus, in The Matrix
Pairs of countable things are themselves countable. In other words: Any pair of integers can be associated with a single scalar integer, distinct from the integer representing any other pair.
One way is to raise mutual primes, such as 2 and 3, to the original values, then multiply the results to get a single number, as in the following ‘encode’ function:
This is more powerful than simple addition, multiplication, or exponentiation, because it’s guaranteed to be reversible. We can recover the inputs by factoring, as in this ‘decode’ function:
For example, we can encode the pair (3, 5) as the single value 1944, because 2**3 = 8, 3**5 = 243, and 8 * 243 = 1944:
Let’s take this trick for a spin on everyone’s favorite hobbyhorse, the Fibonaccis.
The Fibonacci sequence (OEIS A000045) is a well known plaything of mathematicians and programmers alike. It begins [0, 1], and each subsequent number is the sum of the previous two. The first ten Fibonacci numbers are therefore [0, 1, 1, 2, 3, 5, 8, 13, 21, 34]:
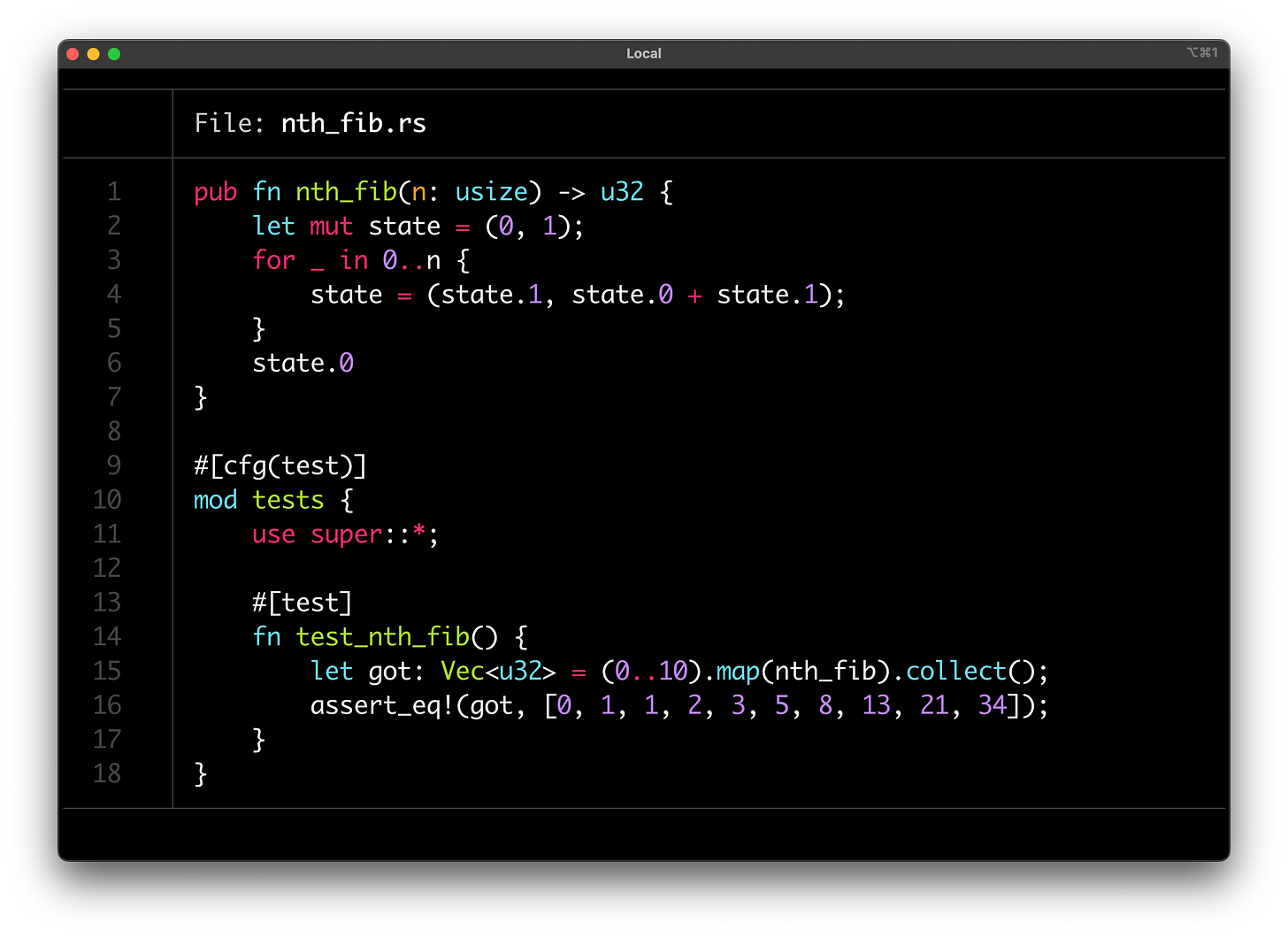
A loop for generating Fibonacci numbers obviously must maintain two integer values as state, because, by definition, it needs them to compute the next value:
But using our handy integer compression trick, we can amaze friends and family by implementing a Fibonacci loop that maintains only a single integer between iterations!
Can we repeat the process, reducing any four values into two scalars, and thence to a single integer? By extension, can we compress arbitrary amounts of data into a single integer? Yes in principle, but no in practice, because the exponentiation quickly causes overflow, or turns BigInts into RAM hogs.
Does this trick have any practical application at all? None whatsoever, as far as I know. It’s just cool enough that I thought you should know about it. 😎