Recursion Stinks

see also: Recursion Stinks

This is a code-heavy post. Code is presented as images to preserve formatting and highlighting, with captions linked to plain text files.

---

I always ask software engineering interview candidates to implement a factorial function, then (assuming factorial goes well) a Fibonacci function. These are admittedly trite exercises that, for senior engineers, serve as quick warm-ups. Junior engineers didn’t used to have much trouble with them, either; but over the past ~10 years, a strange trend has arisen whereby new college grads consistently go straight for recursive implementations. They all seem to do this. It’s uncanny. (Are entry-level software engineers all reading the same prep book, or watching the same YouTube channel or something?) Recursion usually makes for terrible solutions, and I’d like to show you some reasons why.

🪤 Despite The Problem with Big O, this post bears a light sprinkling of big-O expressions. It’s fine to skip right past them if you want. Moreover, we’ll distinguish space and time complexity using ‘s’ and ‘t’ subscripts; for example, Oₛ(N)Oₜ(2ᴺ) indicates that an algorithm completes in linear space and exponential time. But again, it’s fine to ignore all that, unless you’re a glutton for undergrad-level Computer Science.

Factorial

First, let’s look at a recursive factorial function. We’ll use Rust, but (except where noted) the same principles hold for other languages.

Recursive factorial function: Oₛ(N)Oₜ(N) (factorial_rec.rs)

The first thing that should concern you about this code is integer overflow. Factorials get big fast. Integer overflow is easy enough to avoid (potentially at the expense of performance) by switching to a growable return type like num::BigUint. Some languages, like Python, even use growable integers by default.

The bigger problem is stack overflow. Most programming languages (with notable exceptions like Golang, as explained by Dave Cheney) allow each thread only a finite amount of stack space. Each recursive call takes another chunk out of that space. When the stack space is gone, the program crashes, and it crashes ugly.

A typical stack overflow message (stack-overflow.log)

Some languages (like Scheme, Haskell, and Scala) support Tail Call Elision (TCE), silently optimizing certain functions so they don’t overflow the stack. The implementation above is not amenable to this optimization, and most candidates who jump straight to recursive solutions (or at least, the ones I’ve asked) can’t even explain what a “tail call” is. (The point isn’t that engineers should know about TCE, but that we shouldn’t write code that crashes in the absence of particular optimizations.)

Linear (Oₛ(1)) recursion is exactly the sort of thing that works fine in test code, but blows up in production. Do not recurse in production code unless you have a good reason. Figuring out whether my team will have to explain things like this to new hires is part of the reason I still ask these clichéd, boring questions.

The obvious implementation I would expect most juniors to write—and I swear, they used to do so—is a for-loop:

Looping factorial function: Oₛ(1)Oₜ(N) (factorial_loop.rs)

A plain old loop is absolutely fine for something like factorial. A more sophisticated approach would be to delegate most of the work to a standard library function:

Factorial as a product of 1..=n: Oₛ(1)Oₜ(N) (factorial_product.rs)

Yet another option is a look-up table of precomputed values:

Factorial as an array of precomputed values: Oₛ(N)Oₜ(1) (factorial_table.rs)

None of these solutions is liable to blow the call stack, and all of them have better complexity than the recursive solution. These principles aren’t specific to factorial, either: If you want to be a professional computer programmer, you have to be able to write a for-loop. Don’t get any fancier than that unless you can explain your reasons for doing so.

Fibonacci

The reason I ask Fibonacci, even if someone nails factorial, is that efficient implementation requires a translation from the problem domain to the solution domain. That’s something a candidate will do easily if (and only if) they’re already in the habit.

The Fibonacci sequence, as a mathematical object, is defined recursively:

fib(0) = 0
fib(1) = 1
fib(n) = fib(n - 2) + fib(n - 1)

A naive implementation looks like this:

An expensive way to find the Nth Fibonacci number: Oₛ(N)Oₜ(2ᴺ) (fib_naive.rs)

Aside from the overflow issues we already discussed in the context of factorials, this Fibonacci function has a severe scalability problem in the form of exponential time complexity. This is another great example of something that works fine in tests, but can cause production outages in the real world. Exponential isn’t quite as bad as factorial, but it’s bad enough to ruin your day.

Benchmarking our naive Fibonacci function (benchmark.rs)

Exponential complexity can ruin your day. (benchmark.log)

The complexity here isn’t due to recursion per se, but to a misunderstanding of how we should translate inductive definitions like fib(n) into computer programs where time and space actually matter.

So many good ideas are never heard from again once they embark in a voyage on the semantic gulf.

—Alan Perlis, Epigrams in Programming

The first step is to identify the state that must be passed from one iteration to the next; in other words, the signature of the recursive function. For Fibonacci, the state is the most recent two results, and the number of iterations remaining. Here’s a linear complexity (tail-)recursive Fibonacci implementation:

Linear-time recursive Fibonacci function: Oₛ(N)Oₜ(N) (fibonacci_rec.rs)

When candidates who’ve implemented the naive solution above are asked to address the exponential complexity, they always—and I mean, always—try adding a cache, effectively memoizing the function. That gets us back down to linear space and time (Oₛ(N)Oₜ(N)), but a simple loop would run in constant space and linear time:

Nth Fibonacci via for-loop: Oₛ(1)Oₜ(N) (fibonacci_loop.rs)

Higher Order Functions

Students of Functional Programming spend their first year learning to recurse, and their second year learning not to.

—Unknown

Much as factorial can be expressed as the product of a range of integers, a more sophisticated Fibonacci implementation might use a Higher Order Function (HOF) like successors:

Fibonaccis from a Higher Order Function (fibonacci_hof.rs)

Using HOFs instead of hand-rolled loops is a pretty strong indicator that this ain’t the author’s first rodeo. (Similar HOFs exist in most languages, or else can be easily implemented using iterators or generator functions. For example, what Rust calls ‘successors,’ Haskell and Clojure both call ‘iterate.’)

Higher order functions are often even better than loops, for two main reasons:

1. They express your intent directly. A loop that processes elements of one array and adds them to another is rarely as clear as a call to map and/or filter (or an equivalent comprehension in Haskell, Scala, or Python). Such direct expression of intent makes the code easier to work with for both humans and compilers.

   In some cases for_each may also be faster than a loop, because it will use internal iteration on adapters like Chain.
   —Trait std::iter::Iterator

2. They’re more composable, enabling you to share low-level functionality across functions.

Suppose we want to know how many Fibonacci numbers are below a given value. If we start from the ‘fibonacci_loop’ function above, there’s no good way to factor out the loop logic itself. We’re stuck writing a completely new, though conceptually very similar loop.

Each new loop entails redundant logic (fibonacci_loop_count_below.rs)

With the HOF based version, though, we can easily factor out not only the iteration, but the iteration state; in this case, keeping the value ‘b’ out of the caller’s scope.

Three functions concisely sharing functionality (fibonacci_hof_count_below.rs)

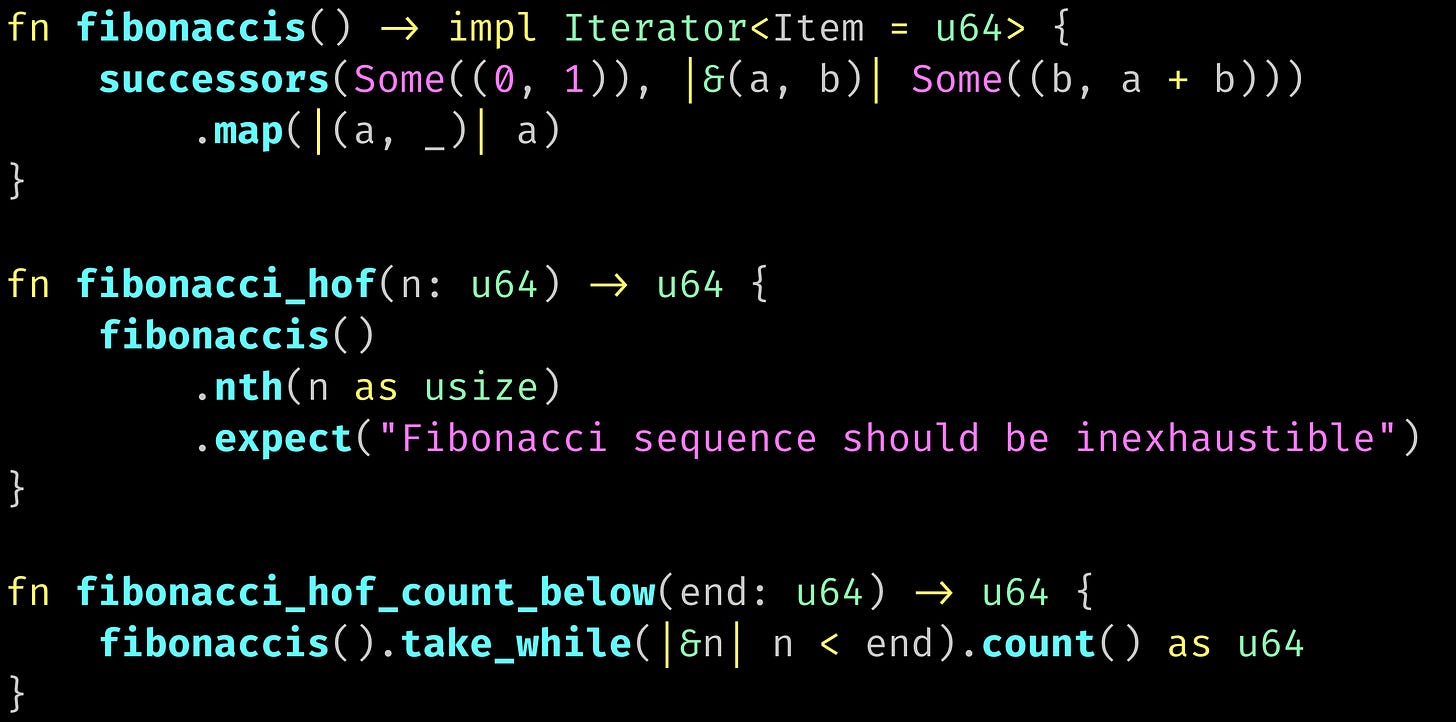
Some technical leaders take the preference for HOFs to the extreme. Others positively fetishize raw loops. My own experience is that HOFs are almost always the best option. They scale better than loops, both within individual programs, and as library features. They also tend to go hand in hand with short variable names, and let you mentally separate mechanics from semantics; e.g., separating loop logic (I have a list, and want the Nth item) from the business domain (I’m implementing a Dutch auction, and need the second-highest bid).

But, the glue required to match HOF callback signatures—for example, in our HOF-based Fibonacci functions above, the Some() and .expect() calls—is a pain for small examples. It’s often best to start with a short hand-written loop, but replace it with a HOF at the very first sign of complexity.

OK, fine, recursion is occasionally useful

When, if ever, should you use recursion? Here’s a fancy Fibonacci function I wrote a long time ago that recurses instead of looping. I felt OK writing that because it runs in logarithmic, rather than linear, time and space (Oₛ(log N)Oₜ(log N)). Recursion is also a convenient way to get a data stack for free, if you’re willing to abuse the call stack to hold data; for example, when traversing a binary tree. Even then, it’s usually better to use an explicit stack.

💡 The only difference between depth-first and breadth-first search is whether newly encountered nodes are added to a stack (LIFO) or a queue (FIFO).

If you know what you’re doing and why, then it’s OK for recursion to be one of the tools in your toolbox. It is not, however, a good idea to recurse where a loop or HOF would suffice merely because recursion is what the cool kids seem to be doing.